3.3 Paramagnetism¶
Introduction¶
You may have heard of infinite or negative temperatures. This seems rather odd, and is probably hard to get your head around, but if you change your perspective about temperature, and think instead about entropy, these things will make sense.
Although the actual situations in which infinite or negative energies may arise are specific to very controlled laboratory experiments, it teaches us about some fundamental properties of entropy and temperature.
Review¶
Entropy is defined as
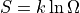 , where
, where
 is the multiplicity of a given state. Typically, that is the
number of ways you can arrange a specific total internal energy. For most materials,
entropy tends to move up and to the right, logarithmically.
is the multiplicity of a given state. Typically, that is the
number of ways you can arrange a specific total internal energy. For most materials,
entropy tends to move up and to the right, logarithmically.The 2nd Law of Thermodynamics is that entropy increases over time. Energy will flow so that entropy will maximize. This is not a fundamental law, but we will treat it as such. (The fundamental rule is that random things randomize.)
Temperature is defined as
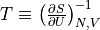 . That is, it is inversely proportional to the change of
entropy over internal energy, keeping the volume and number of particles
constant. A way to think of this is it is the willingness of the material to
“share” energy so that entropy can be maximized. High temperature objects
aren’t getting a lot of entropy per unit energy, and low temperature objects
would get a lot of entropy for a little bit of energy, so energy flows from
the high temperature object to the low temperature object in order to
increase entropy. When two objects would increase the same amount of entropy
for a given amount of energy, they are in thermal equilibrium, and there is
no longer a net flow of energy between them.
. That is, it is inversely proportional to the change of
entropy over internal energy, keeping the volume and number of particles
constant. A way to think of this is it is the willingness of the material to
“share” energy so that entropy can be maximized. High temperature objects
aren’t getting a lot of entropy per unit energy, and low temperature objects
would get a lot of entropy for a little bit of energy, so energy flows from
the high temperature object to the low temperature object in order to
increase entropy. When two objects would increase the same amount of entropy
for a given amount of energy, they are in thermal equilibrium, and there is
no longer a net flow of energy between them.The heat capacity of an object is defined as
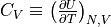 . All objects should tend to 0
heat capacity as temperature approaches 0, which is the third law of
thermodynamics. The heat capacity describes how the internal energy would
need to change to reflect a change in temperature. (When we get into
infinite and negative temperatures, we’ll see some strange heat capacities
as well.)
. All objects should tend to 0
heat capacity as temperature approaches 0, which is the third law of
thermodynamics. The heat capacity describes how the internal energy would
need to change to reflect a change in temperature. (When we get into
infinite and negative temperatures, we’ll see some strange heat capacities
as well.)
Health Check¶
At this point, I want to issue a “health check”. If you are taking this course, and you feel like you are getting lost, or you have taken an exam on this material, and you did poorly, then it’s time to assess where you are at.
99% of the time, when I was tutoring students, I found that there were gaps in their understanding. Perhaps this is because they missed something, or forgot it. More likely, they tackled previous chapters and barely understood the material. Without a firm grasp of previous content, this section is going to be almost impossible to understand.
My recommendation is to go back and review! Review the chapters, watch the lectures again, and do the homework problems again. If you have failed an exam, take apart each question you got wrong and understand why you got it wrong, and master those concepts you missed.
As with any advanced physics course, this material isn’t impossible to understand! I like to say “It doesn’t take a genius to get this” but in reality, sometimes we are victims of our own ingeniuty. Meaning, we are able to “glide” through earlier sections because we know how to derive results. At this point, you shouldn’t be deriving results, but the results should’ve been memorized and internalized. So don’t rely on your genius – rely on your memory and your experience.
Paramagnetism¶
Remember in the last section where we listed out the “five steps” to calculate entropy, temperature, and heat capacity? We talked about how there’s only a handful of problems that allow us to proceed rigorously through those five steps, and for everything else, we can work backwards, starting with heat capacity, and eventually calculate the entropy by experiment only.
Paramagnetism is one of those handful of cases where we can actually calculate the multiplicity, entropy, temperature, and heat capacity. The results, however, should be fairly surprising. Indeed, because of the surprises here, I am of the mind that perhaps temperature should be redefined to be the inverse of what it is today – the “greediness” of objects, rather than their “generosity” – going back to the “Silly Analogy” of section 3.1.
The case is called the “two-state paramagnet” and it arises in nature in very specific circumstances.
Notation¶
In order to make the math easier to understand, we’re going to use a specific notation system.
When you have a system of  spin-1/2 particles immersed in a constant
magnetic field
spin-1/2 particles immersed in a constant
magnetic field 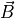 pointing in some direction (we’ll use the
pointing in some direction (we’ll use the
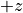 direction), each particle will try to align with the field. We call
particles like this “dipoles”, not unlike electric diploes, which are pulled
to conform with electric fields.
direction), each particle will try to align with the field. We call
particles like this “dipoles”, not unlike electric diploes, which are pulled
to conform with electric fields.
We’re ignoring any interaction between particles, because the math is a lot easier and also because the interaction ends up being negligible.
Due to quantum mechanics, they can either align with the field, or against it. We say “spin up” or “spin down”. “Spin up” means the dipole is aligned, and “spin down” means it is opposed.
When the dipole is in spin up, then it is in a lower energy state than spin down. At this point, we get to choose where “0 energy” is, because, as you should be aware by now, it doesn’t matter where you set your 0-point for energy. There are two obvious and good choices: either “spin up” is zero energy, or halfway between spin up and spin down is zero energy. We’re going to choose halfway between as the zero point, so the energies are:
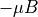 when spin up.
when spin up.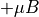 when spin down.
when spin down.
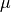 is just a constant reflecting how “strong” the dipole is – its
magnetic moment.
is just a constant reflecting how “strong” the dipole is – its
magnetic moment.
With this, we can count the total energy, using 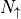 for the
number of particles in spin up, and
for the
number of particles in spin up, and 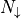 for the number of
particles in spin down.
for the number of
particles in spin down.
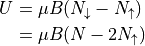
(Note that 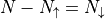 .)
.)
The total magnetic moment 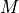 is written as:
is written as:
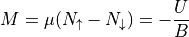
The multiplicity for a state described by the total number of spin up particles is:
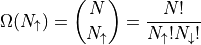
Note that the multiplicity is the same if you switch all the ups with downs.
Numerical Solution¶
At this point, Schroeder builds a table listing what happens when you have 100 dipoles. I won’t reproduce the table here, but I will note a few very interesting properties that should be somewhat surprising.
It is very important that you understand what the columns are saying. The columns are:
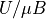 . This is just the internal energy scaled into units by
removing the dipole moment and the magnetic field strength.
. This is just the internal energy scaled into units by
removing the dipole moment and the magnetic field strength.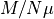 is the magnetic moment of the entire thing, scaled into units
by removing the dipole moment and number of particles.
is the magnetic moment of the entire thing, scaled into units
by removing the dipole moment and number of particles. , the multiplicity. How many ways that the system of that many
spin-up and spin-down dipoles can be arranged.
, the multiplicity. How many ways that the system of that many
spin-up and spin-down dipoles can be arranged.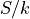 , the entropy, scaled into units by removing the Boltzmann
constant.
, the entropy, scaled into units by removing the Boltzmann
constant.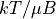 . the temperature, again scaled into units by removing the
Boltzmann constant, dipole moment, and magnetic field strength.
. the temperature, again scaled into units by removing the
Boltzmann constant, dipole moment, and magnetic field strength.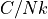 , the heat capacity, scaled to units by removing the number of
particles and Boltzmann constant.
, the heat capacity, scaled to units by removing the number of
particles and Boltzmann constant.
Looking at the chart, we see the following:
As you flip more dipoles to spin down, the internal energy increases, along with the magnetic moment. This is expected. However, at some point, there are no more dipoles to flip, so there is a maximum energy that can be contained by the dipoles. (We didn’t see this with the einstein solid and ideal gas – you could just keep adding more and more energy to those!)
The multiplicity reaches a maximum when the energy is zero – half spin up, half spin down. Any more energy added after this point actuall decreases the entropy.
The temperature of the paramagent increases as you add energy, until you hit the halfway point. At that point, the energy is infinite. Adding more energy will cause the temperature to become negative.
The heat capacity starts at 0 at the lowest energy, increases, but then decreases back to 0 at the half-way point. Then it increases again and falls back to zero at maximum energy.
Infinite temperature? Negative temperature? What does it mean?
In order to fully grasp this, let’s look at figure 3.8 – the relationship between entropy and internal energy. As we see, it forms a sort of half-circle. Entropy is maximized at the half-way point. Near the extremes, entropy rises or falls rapidly, while it steadies out near the middle.
In our “Silly Analogy”, what does this material represent? It behaves “normally” as long as it is below the halfway point. As it reaches the halfway point, it would love to share its energy, since it gets practically no entropy from it. If it goes beyond the halfway point, it will share its energy with anything that will even slightly increase its entropy with more energy, because it increases in entropy by losing energy.
Let’s put on top of this graph a graph of the temperature versus the internal energy. You’ll note that the temperature rapidly increases as we reach the midpoint – which is what we expected, as it’s not getting much entropy with more energy, so it is more than ready to shed entropy to maximize entropy.
At the midpoint, things go crazy.
Beyond the midpoint, we see the sort of thing we expect to see in hyperbolic graphs. This is entirely due to the fact that temperature is an inverse of some other thing – the derivative of entropy with respect to internal energy – and so it shows its quirkiness here.
To summarize:
Infinite temperature occurs when adding or removing energy doesn’t change the entropy at all. These objects are going to shed energy to any “normal” object, and are thus “hotter than anything else in the universe”.
Negative temperatures occur when removing energy increases entropy. These objects will shed energy to any “normal” object, and will even shed energy to things with infinite temperature, and even shed energy to things with lower negative energy.
Negative zero temperature is a temperature that is hotter than anything else. You can’t add any more energy to it, as nothing will transfer energy into it and it can’t even store that energy.
Thus, you can think of temperatures as arranged in sequence of colder to hotter as:
Absolute zero
Normal temperatures from absolute zero and up to infinity.
Very large negative temperatures, and then up to zero.
Actual experiments have been performed, and the magnetic field has been flipped (to switch the temperature to negative) and this conforms with reality.
Problem 3.17¶
Fill in the 3rd line of the table.
Problem 3.18¶
Use a computer to derive the table and graphs.
Analytic Solution¶
Using Stirling’s approximation, along with the assumption that all the numbers of particles is large (total, spin up, spin down):
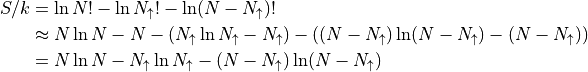
Problem 3.19 is to work out the rest of the math yourself. Here are the conclusions.
For temperature, we will use the chain rule.
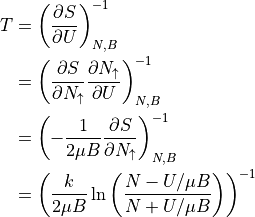
When U>0, then the log has a larger bottom than top, so T is negative. When U < 0, then the log has a larger top than bottom, to T is positive. U and T always have opposite signs.
Rewriting U in terms of T:
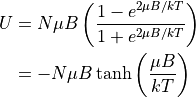
Calculating M:

tanh is the hyperbolic tangent. As a refresher (as you likely haven’t seen these before):
Hyperbolic sine is
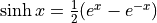 . We pronounce
it “sinsh”
. We pronounce
it “sinsh”Hyperbolic cosine is
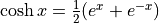 . We pronounce
it “cosh”
. We pronounce
it “cosh”Hyperbolic tangent is
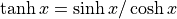 . We pronounce it
“tansh”.
. We pronounce it
“tansh”.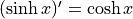
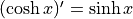
The graph of tanh is shown in the book. It starts at -1 on the left, rises slowly and then crosses the y-axis with a slope of 1 and then settles at 1 on the right.
Heat capacity:
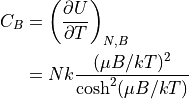
Note that this approaches zero at either low or high temperature, and it has a trough around T=0.
Electronic Dipoles¶
You can get a magnetic dipole if there is an unpaired electron. The electrons will normally “cancel” each other’s spins out. The unpaired electron will have orbital and spin angular momentum, and so will have two possible dipole moments (and 4 combinations of up and down therein). In some environments, the orbital moment is quenched by neighboring atoms, leaving only the spin angular momentum.
For such a case, the Bohr Magneton describes the situation:
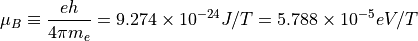
In a 1 T field (a very strong magnetic field) you can get 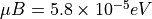 . At room temperature,
. At room temperature, 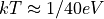 , so
, so
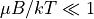 . At this limit,
. At this limit, 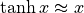 so:
so:
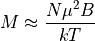
It was Pierre Curie who discovered the inversely proporation relationship between temperature and the magnetic moment and this is called Curie’s Law. It holds even for all paramagnets in the high temperature limit (IE, not cryogenic temperatures), even those with orbital angular momentum. In such systems, the heat capacity is inversely proportional to the square of the temperature.
Nuclear Dipoles¶
If you were to consider nuclear dipoles, replacing the mass of the electron
with the mass of a proton will get you a 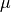 that is 2,000 times as
large. This means that to compensate, you need a field 2,000 times as strong
(which is impossible to build) or temperatures that are 2,000 times lower. In
practice, you need to get the temperatures down to a few millikelvin to see
the strange behavior.
that is 2,000 times as
large. This means that to compensate, you need a field 2,000 times as strong
(which is impossible to build) or temperatures that are 2,000 times lower. In
practice, you need to get the temperatures down to a few millikelvin to see
the strange behavior.
Problem 3.19¶
Do the math.
Problem 3.20¶
Calculate energy, magnetization, and entropy of the DPPH example.
Problem 3.21¶
Calculate the energy and wavelength of a photon that can detect the magnetization of the nuclear material in Purcell’s and Pound’s experiment.
Problem 3.22¶
Sketch or use a computer to plot the entropy vs. temperature of a two-state paramagnet. How would it change if you varied the magnetic field strength B?
Problem 3.23¶
Calculate the formula the entropy of a two-state paramagnet as a function of temperature. Check that it behaves as you’d expect as T approaches 0 and T approaches infinity.
Problem 3.24¶
This and Problem 3.25 are “extremely importnat”. I may do a video on them.
Use a computer to build a table for an einstein solid and compare your results with lead, aluminum, and diamond.
Problem 3.25¶
A lot of math, leading up to “when the smoke clears.”
Problem 3.26¶
Shows that it can apply to vibrational modes as well.

